Algorithm and Data Structure Summary

, , ,

算法与数据结构汇总

Big-O Concept

{O 上界} {Ω Omega 下界} {Θ Theta 上下界}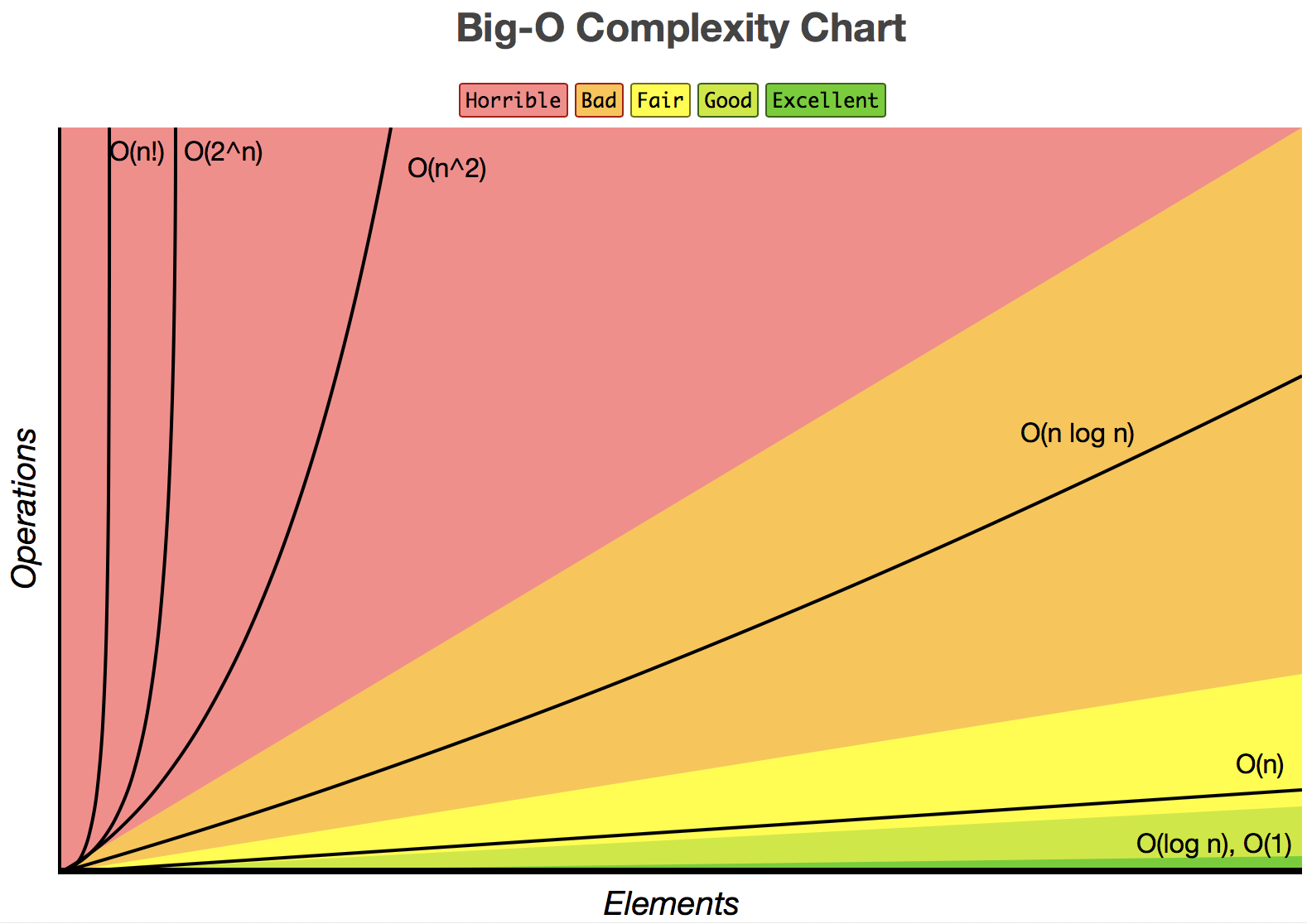
big_o_complexity

Sorting Algorithm Complexity

sort_algorithm_complexity
sorting_algo_gif (credit to: https://www.toptal.com/developers/sorting-algorithms/)

Data Structure 数据结构

array 数组

  • 特性
    • ordered
    • random-access (constant O(1) time access)
    • get_length - O(1)
    • append_last - O(1)

dictionary 字典

key-value hashable

1
2
# python
scores = {"Eric": 90, "Mark": 80, "Wayne": 60}
1
2
// swift
var scores: [String: Int] = ["Eric": 90, "Mark": 80, "Wayne": 60]

linked list 链表

benefit: can add and remove items from the beginning of the list in constant time.

singly linked list 单向链表, doubly linked list 双向链表

  • runer technique: iterate through the linked list with two pointers simultaneously (fast and slow)
1
2
3
4
5
6
7
8
9
10
11
12
13
# python
# singly linked list 单向链表
class SinglyLinkedListNode:
    def __init__(self, value, next=None):
        self.val = value
        self.next = next

# doubly linked list 双向链表
class DoublyLinkedListNode:
    def __init__(self, value, next=None, prev=None):
        self.val = value
        self.next = next
        self.prev = prev
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
// swift
// singly linked list 单向链表
public class SinglyLinkedListNode<Value> {
    public var value: Value
    public var next: SinglyLinkedListNode?

    public init(value: Value, next: SinglyLinkedListNode?=nil) {
        self.value = value
        self.next = next
    }
}

// doubly linked list 双向链表
public class DoublyLinkedListNode<Value> {
    public var value: Value
    public var next: DoublyLinkedListNode?
    public var prev: DoublyLinkedListNode?

    public init(value: Value, next: DoublyLinkedListNode?=nil, prev: DoublyLinkedListNode?=nil) {
        self.value = value
        self.next =next
        self.prev = prev
    }
}

set 集合

unordered collecition of unique values

  • dic 字典
  • hashtable
1
2
3
# python
my_set = set([1,2])    # + - & | ^
empty_set = set()
1
2
3
// swift
var my_set: Set<Int> = [1, 2]
var my_set2 = Set<Int>()

list 列表

stack queue priority queue heap

stack 栈

{LIFO} {push, pop, top, isEmpty}

1
2
3
4
# python
stack = [1, 2, 3]
stack.append(4)
num = stack.pop()   # >>> 4
1
2
3
4
5
6
7
8
9
10
// swift
public struct Stack<E> {
    private var stack: [E] = []
    public mutating func push(_ element: E) {
        stack.append(element)
    }
    public mutating func pop() -> E? {
        return stack.popLast()
    }
}

queue 队列

{FIFO} {enqueue, dequeue, front, rear, isEmpty}

  • can be created in four ways:
    • array - {dequeue in this struct takes O(n)}
    • doubly linked list - {elements aren’t in contiguous blocks of memory. will increase access time}
    • ring buffer - {fixed size}
    • two stacks - {best}
1
2
3
4
5
6
7
# python3
# double ended queue
# deque 在首尾两端快速插入和删除而设计
from collections import deque
queue  = deque([1, 2, 3])
queue.append(4)
queue.popleft()
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
// swift
public struct QueueStack<T>: Queue {
    private var leftStack: [T] = []
    private var rightStack: [T] = []
    public init() { }

    public var isEmpty: Bool {
        return leftStack.isEmpty && rightStack.isEmpty
    }

    public var peek: T? {
        return !leftStack.isEmpty ? leftStack.last : rightStack.first
    }

    public mutating func enqueue(_ element: T) -> Bool {
        rightStack.append(element)
        return true
    }

    public mutating func dequeue() -> T? {
        if leftStack.isEmpty {
            leftStack = rightStack.reversed()
            rightStack.removeAll()
        }
        return leftStack.popLast()
    }
}
priority queue 优先队列
heap 堆

can also be developed in tree structure
[]

graph 图

{G = <V-vertex, E-edge>} {directed, undirected ,weighted, unweighted}

  • complete graph 完全图
  • dense graph 稠密图
  • spares graph 稀疏图
  • {表示方法: adjacency matrix邻接矩阵 - 适合稠密图 & adjacency lists邻接链表 - 适合稀疏图}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
# python
class AdjacencyList:
    def __init__(self):
        self.a_list = {}

    def addEdge(self, from_vertex, to_vertex):
        if from_vertex in self.a_list.keys():
            self.a_list[from_vertex].append(to_vertex)
        else:
            self.a_list[from_vertex] = [to_vertex]

    def print_a_list(self):
        for from_v in self.a_list:
            print('{vertex} ->'.format(vertex = from_v), ' -> '.join(
                  [str(to_v) for to_v in self.a_list[from_v]]))

tree 树

{|E| = |V| - 1}

  • tree
  • binary tree
  • binary search tree (BST) 二叉查找树 {math.floor(logn) <= h <= n-1}
  • balanced search tree 平衡查找树
    • self-balancing 自平衡查找树
      • AVL tree
        • 每个节点的左右子树高度差不超过1
      • red-black tree 红黑树
        • 能容忍同一节点的一棵子树的高度是另一棵子树的两倍
      • splay tree 分裂树
    • 允许单个节点中包含不只一个元素
      • 2-3 tree
      • 2-3-4 tree
      • B tree
  • complete binary tree 完全二叉树
  • heap (binary heaps) {complete binary tree}
    • 可以用完全二叉树实现, 树的每一层都是满的，除了最后一层最右边元素可能缺位
    • 父母优势, 每一个节点的键都要大于等于它子女的键
1
2
3
4
5
     10
   /    \      if using array:
  8      7          parents  leaves
 / \    / \     0   1  2  3| 4  5  6
5   2  6       [ , 10, 8, 7, 5, 2, 6]
  • Trie tree (prefix trees) 单词查找树
    1
    2
    3
    4
    5
        root
       /    \
      T      C
     / \    / \
    R.  O. A.  O.

tree

1
2
3
4
5
6
7
# python
class TreeNode:
    def __init__(self, value):
        self.val = value
        self.children = []
    def add(child):
        children.append(child)
1
2
3
4
5
6
7
8
9
10
11
// swift
public class TreeNode<T> {
    public var value: T
    public var children: [TreeNode] = []
    public init(_ value: T) {
        self.value = value
    }
    public func add(_ child: TreeNode) {
        children.append(child)
    }
}

binary tree 二叉树

1
2
3
4
5
6
# python
class BinaryTreeNode:
    def __init__(self, value):
        self.val = value
        self.left = None
        self.right = None
1
2
3
4
5
6
7
8
9
10
// swift
public class BinaryTreeNode<Element> {
    public var val: Element
    public var left: BinaryTreeNode?
    public var right: BinaryTreeNode?

    public init(value: Element) {
        self.val = value
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
// swift
// draw the tree
extension BinaryTreeNode: CustomStringConvertible {
    public var description: String {
        return diagram(for: self)
    }

    private func diagram(for node: BinaryTreeNode?,
                         _ top: String = "",
                         _ root: String = "",
                         _ bottom: String = "") -> String {
        guard let node = node else {
            return root + "nil\n"
        }
        if node.left == nil && node.right == nil {
            return root + "\(node.val)\n"
        }
        return diagram(for: node.right, top + " ", top + "┌──", top + "│ ")
            + root + "\(node.val)\n"
            + diagram(for: node.left, bottom + "│ ", bottom + "└──", bottom + " ")
    }
}

Note: This BinaryTreeNode discription algorithm from Optimizing Collections

  • tree traversal
    • preorder (左中右)
    • inorder （中左右)
    • postorder (左右中)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
def preorder(tree):
    if tree:
        print(tree.val)
        preorder(tree.left)
        preorder(tree.right)
def inorder(tree):
    if tree:
        inorder(tree.left)
        print(tree.val)
        inorder(tree.right)
def postorder(tree):
    if tree:
        postorder(tree.left)
        postorder(tree.right)
        print(tree.val)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
// swift
extension BinaryTreeNode {
    public func preOrder(visit: (Element) -> ()) {
        visit(val)
        left?.preOrder(visit: visit)
        right?.preOrder(visit: visit)
    }
    public func inOrder(visit: (Element) -> ()) {
        left?.inOrder(visit: visit)
        visit(val)
        right?.inOrder(visit: visit)
    }
    public func postOrder(visit: (Element) -> ()) {
        left?.postOrder(visit: visit)
        right?.postOrder(visit: visit)
        visit(val)
    }
}

binary search tree (BST) 二叉查找树

math.floor(logn) <= h <= n-1
fast lookup, addition, and removal operations: O(logn)

  • value of left child less than its parent
  • value of right child greater than or equal to its parent
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
# python
class BinaryTreeNode:
    def __init__(self, value):
        self.val = value
        self.left = None
        self.right = None

    def inorder(self, visit):
        if self.left:
            self.left.inorder(visit)
        visit(self.val)
        if self.right:
            self.right.inorder(visit)

    def get_min(self):
        min = self
        while min.left:
            min = min.left
        return min

    def __repr__(self):
        def diagram(node, top="", root="", bottom=""):
            if not node:
                return root + "None\n"
            if (not node.left) and (not node.right):
                return root + str(node.val) + '\n'
            return (diagram(node.right, top + ' ', top + '┌──', top + '│ ')
                   + root + str(node.val) + '\n'
                   + diagram(node.left, bottom + '│ ', bottom + '└──', bottom + ' '))
        return diagram(self)

class BinarySearchTree:
    def __init__(self):
        self.root = None

    def insert(self, val):
        self.root = self.__insert(self.root, val)

    def __insert(self, node, val):
        if not node:
            return BinaryTreeNode(val)
        if val < node.val:
            node.left = self.__insert(node.left, val)
        else:
            node.right = self.__insert(node.right, val)
        return node

    def contain(self, val):
        current = self.root
        while current:
            if current.val == val:
                return True
            if val < current.val:
                current = current.left
            else:
                current = current.right
        return False

    def remove(self, val):
        self.root = self.__remove(self.root, val)

    def __remove(self, node, val):
        if not node:
            return None
        if val == node.val:
            if (not node.left) and (not node.right):
                return None
            if node.right:
                return node.right
            if node.left:
                return node.left
            node.val = node.right.get_min().val
            node.right = self.__remove(node.right, node.val)
        elif val < node.val:
            node.left = self.__remove(node.left, val)
        else:
            node.right = self.__remove(node.right, val)
        return node

    def inorder(self, root, visit):
        if root:
            self.inorder(root.left, visit)
            visit(root.val)
            self.inorder(root.right, visit)

    def __repr__(self):
        return str(self.root)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
// swift
public class BinaryTreeNode<Element> {
    public var val: Element
    public var left: BinaryTreeNode?
    public var right: BinaryTreeNode?

    public init(value: Element) {
        self.val = value
    }

    // get the min node of the BTS
    var min: BinaryTreeNode {
        return left?.min ?? self
    }
}

extension BinaryTreeNode: CustomStringConvertible {
    // ...
    // same as extension in binary tree
}

public struct BinarySearchTree<Element: Comparable> {
    public private(set) var root: BinaryTreeNode<Element>?

    public init() { }
}

extension BinarySearchTree {
    public mutating func insert(_ val: Element) {
        root = insert(from: root, val: val)
    }

    private func insert(from node: BinaryTreeNode<Element>?, val: Element) -> BinaryTreeNode<Element> {
        guard let node = node else {
            return BinaryTreeNode(value: val)
        }
        if val < node.val {
            node.left = insert(from: node.left, val: val)
        } else {
            node.right = insert(from: node.right, val: val)
        }
        return node
    }

    public func contains(_ value: Element) -> Bool {
        var current = root
        while let node = current {
            if node.val == value {
                return true
            }
            if value < node.val {
                current = node.left
            } else {
                current = node.right
            }
        }
        return false
    }

    public mutating func remove(_ value: Element) {
        root = remove(node: root, value: value)
    }

    private func remove(node: BinaryTreeNode<Element>?, value: Element) -> BinaryTreeNode<Element>? {
        guard let node = node else {
            return nil
        }
        if value == node.val {
            if node.left == nil && node.right == nil {
                return nil
            }
            if node.left == nil {
                return node.right
            }
            if node.right == nil {
                return node.left
            }
            node.val = node.right!.min.val
            node.right = remove(node: node.right, value: node.val)
        } else if value < node.val {
            node.left = remove(node: node.left, value: value)
        } else {
            node.right = remove(node: node.right, value: value)
        }
        return node
    }
}

extension BinarySearchTree: CustomStringConvertible {
    public var description: String {
        return root?.description ?? "empty tree"
    }
}

AVL Tree

self-balancing binary search tree

  • Rotations
    • left
    • right-left
    • right
    • left-right
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
# python
__author__ = 'Min'
class AVLTreeNode:
    def __init__(self, value):
        self.val = value
        self.left = None
        self.right = None
        self.height = 0

    def get_min(self):
        min = self
        while min.left:
            min = min.left
        return min

    def get_balanceFactor(self):
        return self.get_left_height() - self.get_right_height()

    def get_left_height(self):
        return self.left.height if self.left else -1

    def get_right_height(self):
        return self.right.height if self.right else -1

    def __repr__(self):
        def diagram(node, top="", root="", bottom=""):
            if not node:
                return root + "None\n"
            if (not node.left) and (not node.right):
                return root + str(node.val) + '\n'
            return (diagram(node.right, top + ' ', top + '┌──', top + '│ ')
                   + root + str(node.val) + '\n'
                   + diagram(node.left, bottom + '│ ', bottom + '└──', bottom + ' '))
        return diagram(self)

class AVLTree:
    def __init__(self):
        self.root = None

    def insert(self, val):
        self.root = self.__insert(self.root, val)

    def __insert(self, node, val):
        if not node:
            return AVLTreeNode(val)
        if val < node.val:
            node.left = self.__insert(node.left, val)
        else:
            node.right = self.__insert(node.right, val)
        balanced_node = self.balanced(node)
        balanced_node.height = max(balanced_node.get_left_height(),
                                   balanced_node.get_right_height()) + 1
        return balanced_node

    def left_rotate(self, node):
        pivot = node.right
        node.right = pivot.left
        pivot.left = node
        node.height = max(node.get_left_height(), node.get_right_height()) + 1
        pivot.height = max(pivot.get_left_height(), pivot.get_right_height()) + 1
        return pivot

    def right_rotate(self, node):
        pivot = node.left
        node.left = pivot.right
        pivot.right = node
        node.height = max(node.get_left_height(), node.get_right_height()) + 1
        pivot.height = max(pivot.get_left_height(), pivot.get_right_height()) + 1
        return pivot

    def right_left_rotate(self, node):
        if not node.right:
            return node
        node.right = self.right_rotate(node.right)
        return self.left_rotate(node)

    def left_right_rotate(self, node):
        if not node.left:
            return node
        node.left = self.left_rotate(node.left)
        return self.right_rotate(node)

    def balanced(self, node):
        if node.get_balanceFactor() == 2:
            if node.left and node.left.get_balanceFactor() == -1:
                return self.left_right_rotate(node)
            else:
                return self.right_rotate(node)
        if node.get_balanceFactor() == -2:
            if node.right and node.right.get_balanceFactor() == 1:
                return self.right_left_rotate(node)
            else:
                return self.left_rotate(node)
        return node

    def contain(self, val):
        current = self.root
        while current:
            if current.val == val:
                return True
            if val < current.val:
                current = current.left
            else:
                current = current.right
        return False

    def remove(self, val):
        self.root = self.__remove(self.root, val)

    def __remove(self, node, val):
        if not node:
            return None
        if val == node.val:
            if (not node.left) and (not node.right):
                return None
            if node.right:
                return node.right
            if node.left:
                return node.left
            node.val = node.right.get_min().val
            node.right = self.__remove(node.right, node.val)
        elif val < node.val:
            node.left = self.__remove(node.left, val)
        else:
            node.right = self.__remove(node.right, val)
        balanced_node = self.balanced(node)
        balanced_node.height = max(balanced_node.get_left_height(),
                                   balanced_node.get_right_height()) + 1
        return balanced_node

    def __repr__(self):
        return str(self.root)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
// swift
private func leftRotate(_ node: AVLNode<Element>) -> AVLNode<Element> {
        let pivot = node.right!
        node.right = pivot.left
        pivot.left = node
        node.height = max(node.leftHeight, node.rightHeight) + 1
        pivot.height = max(pivot.leftHeight, pivot.rightHeight) + 1
        return pivot
}

private func rightRotate(_ node: AVLNode<Element>) -> AVLNode<Element> {
    let pivot = node.left!
    node.left = pivot.right
    pivot.right = node
    node.height = max(node.leftHeight, node.rightHeight) + 1
    pivot.height = max(pivot.leftHeight, pivot.rightHeight) + 1
    return pivot
}

private func rightLeftRotate(_ node: AVLNode<Element>) -> AVLNode<Element> {
    guard let right = node.right else {
        return node
    }
    node.right = rightRotate(right)
    return leftRotate(node)
}

private func leftRightRotate(_ node: AVLNode<Element>) -> AVLNode<Element> {
    guard let left = node.left else {
        return node
    }
    node.left = leftRotate(left)
    return rightRotate(node)
}

private func balanced(_ node: AVLNode<Element>) -> AVLNode<Element> {
    switch node.balanceFactor {
    case 2:
        if let left = node.left, left.balanceFactor == -1 {
            return leftRightRotate(node)
        } else {
            return rightRotate(node)
        }
    case -2:
        if let right = node.right, right.balanceFactor == 1 {
            return rightLeftRotate(node)
        } else {
            return leftRotate(node)
        }
    default:
        return node
    }
}

Brute Force 蛮力法

selection sort 选择排序

{无论什么情况排序速度一样快}

  • 从第一个元素开始从它之后找最小的元素与之交换.
  • Time complexity: {Average: Θ(n^2), Worse: O(n^2), Best: Ω(n^2)}
  • Space complexity: {O(1)}
1
2
3
4
5
6
7
def selection_sort(list):
    for i in range(0, len(list) - 1):
        min_num = list[i]
        for j in range(i + 1, len(list)):
            min_num = min(min_num, list[j])
        list[list[i:].index(min_num) + i], list[i] = list[i], min_num
    return list

bubble sort 冒泡排序

{对于差不多排好序的速度很快，可以到达Ω(n)}

  • 比较相邻元素并将最大的元素向后沉直到最后，重复这个步骤
  • Time complexity: {Average: Θ(n^2), Worse: O(n^2), Best: Ω(n)}
  • Space complexity: {O(1)}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
def bubble_sort(list):
    for i in range(len(list) - 1):
        for j in range(len(list) - 1 - i):
            if list[j] > list[j + 1]:
                list[j], list[j + 1] = list[j + 1], list[j]
    return list
def bubble_sort_upgrade(list):
    for i in range(len(list) - 1):
        already_sorted = True
        for j in range(len(list) - 1 - i):
            if list[j] > list[j + 1]:
                list[j], list[j + 1] = list[j + 1], list[j]
                already_sorted = False
        if already_sorted:
            break
    return list

sequential search 顺序查找 线性算法

  • Time complexity: {Average: Θ(n), Worse: O(n), Best: Ω(1)}
  • Space complexity: {O(1)}
1
2
3
4
5
def sequential_search(list, k):
    for i, ele in enumerate(list):
        if ele == k:
            return i
    return -1

dfs 深度优先查找

  • Time complexity: O(|V|+|E|) = O(b^{d})
  • Space complexity: O(|V|)
1
2
3
4
5
6
7
8
9
10
def dfs(graph, start):
    visited, stack, count = [], [start], 0
    while stack:
        vertex = stack.pop()
        count += 1
        visited.append(vertex)
        for v in graph[vertex]:
            if v not in visited + stack:
                stack.append(v)
    return visited, count

bfs 广度优先查找

  • Time complexity: O(|V|+|E|) = O(b^{d})
  • Space complexity: O(|V|) = O(b^{d})
1
2
3
4
5
6
7
8
9
10
def bfs(graph, start):
    visited, queue, count = [], [start], 0
    while queue:
        vertex = queue.pop(0)
        count += 1
        visited.append(vertex)
        for v in graph[vertex]:
            if v not in visited + queue:
                queue.append(v)
    return visited, count

Decrease-And-Conquer 减治法

insertion sort 插入排序

{对于差不多排好序的速度很快，可以到达Ω(n)}

  • 从第二个元素开始向前找到正确的位置插入
  • Time complexity: {Average: Θ(n^2), Worse: O(n^2), Best: Ω(n)}
  • Space complexity: {O(1)}
1
2
3
4
5
6
7
8
9
def insetion_sort(list):
    for i in range(1, len(list)):
        insert_num = list[i]
        j = i - 1
        while j >= 0 and list[j] > insert_num:
            list[j + 1] = list[j]
            j -= 1
        list[j+ 1] = insert_num
    return list

shell sort 希尔排序

  • 通过一个gap来左插入排序(常用方法是从len/2gap开始每次缩小2倍)
  • Time complexity: {Average: Θ(n(logn)^2), Worse: O(n(logn)^2), Best: Ω(nlogn)}
  • Space complexity: {O(1)}
1
2
3
4
5
6
7
8
9
10
11
def shell_sort(list):
    gap = len(list) // 2
    while gap > 0:
        for i in range(gap, len(list)):
            temp = list[i]
            j = i
            while j >= gap and list[j - gap] > temp:
                list[j], list[j - gap] = list[j - gap], temp
                j -= gap
        gap = gap // 2
    return list

generating permutations

  • JohnsonTrotter
    • Time complexity: O(n!)

binary search 折半查找

  • Time complexity: {Average: Θ(logn), Worse: O(logn), Best: Ω(1)}
  • Space complexity: {O(1)}
1
2
3
4
5
6
7
8
9
10
11
def binary_search(sorted_list, target):
    low, high = 0, len(sorted_list) - 1
    while low <= high:
        mid = (low + high) // 2
        if sorted_list[mid] == target:
            return mid
        elif sorted_list[mid] > target:
            high = mid - 1
        else:
            low = mid + 1
    return -1

quick select 快速选择

  • 寻找第k个最小元素,通过划分来实现
  • Time complexity: {Average: Θ(n), Worse: O(n^2), Best: Ω(n)}
  • Space complexity: O(1)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
def quick_select_m(list, start, end, k_th_min):
    s = partition(list, start, end)
    if s == k_th_min - 1:
        return list[s]
    elif s > k_th_min - 1:
        return quick_select_m(list, start, s - 1, k_th_min)
    else:
        return quick_select_m(list, s + 1, end, k_th_min)
def partition(list, start, end):
    pivot = list[start]
    i = start + 1
    j = end
    while True:
        while list[i] <= pivot and i <= j:
            i += 1
        while list[j] >= pivot and j >= i:
            j -= 1
        if i > j:
            break
        list[i], list[j] = list[j], list[i]
    list[start], list[j] = list[j], list[start]
    return j

Divide-And-Conquer 分治法

分解问题，求解子问题，合并自问题的解
T(n) = aT(n/b) + f(n) {a个需要求解的问题，问题被分成b个，f(n)的分解合并时间消耗}
T(n) = O(n^d) if a < b^d or O(n^dlogn) if a = b^d or O(n^log_b(a)) if a > b^d

merge sort 归并排序

{除了heapsort以外唯一BestAveWorst全是O(nlogn)排序算法}

  • 两种实现方法(自顶向下-递归， 自底向上-循环)
  • Time complexity: {Average: Θ(nlogn), Worse: O(nlogn), Best: Ω(nlogn)}
  • Space complexity: {O(n)}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
def merge_sort(list):
    if len(list) > 1:
        list_b = list[:len(list) // 2]
        list_c = list[len(list) // 2:]
        return merge(merge_sort(list_b), merge_sort(list_c))
    else:
        return list
def merge(list_b, list_c):
    list_a = list_b + list_c    #init list_a
    i, j, k = 0, 0, 0
    while i < len(list_b) and j < len(list_c):
        if list_b[i] <= list_c[j]:
            list_a[k] = list_b[i]
            i += 1
        else:
            list_a[k] = list_c[j]
            j += 1
        k += 1
    if i == len(list_b):
        for index in range(j, len(list_c)):
            list_a[k] = list_c[index]
            k += 1
    if j == len(list_c):
        for index in range(i, len(list_b)):
            list_a[k] = list_b[index]
            k += 1
    return list_a

quick sort 快速排序

{pivot的选择对于算法效率至关重要}

  • 不断选择pivot来将元素划分到它的左右来实现
  • Time complexity: {Average: Θ(nlogn), Worse: O(n^2), Best: Ω(nlogn)}
  • Space complexity: {O(nlogn)}
  • pivot每次选第一个在已经排好序的数组上时间效率是O(n^2)
    • 优化方法
      • 使用随机pivot, 平均划分pivot, 快排好后使用插入排序
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
def quick_sort_m(list, start, end):
    if start < end:
        pivot = partition(list, start, end)
        quick_sort_m(list, start, pivot - 1)
        quick_sort_m(list, pivot + 1, end)
    return list
def partition(list, start, end):
    pivot = list[start]
    i = start + 1
    j = end
    while True:
        while list[i] <= pivot and i <= j:
            i += 1
        while list[j] >= pivot and j >= i:
            j -= 1
        if i > j:
            break
        list[i], list[j] = list[j], list[i]
    list[start], list[j] = list[j], list[start]
    return j

Transform-And-Conquer 变治法

  • 预排序解决问题
    • 检查数组中元素的唯一性
    • 算法数组的模式 （一个数组中最多的元素)

heap sort 堆排序

  • 先构建一个堆, 不断的删除最大键，
  • Time complexity: {Average: Θ(nlogn), Worse: O(nlogn), Best: Ω(nlogn)}
  • Space complexity: {O(1)}
1
2
3
4
import heapq
def heap_sort(list):
    heapq.heapify(list)
    return [heapq.heappop(list) for i in range(len(list))]

problem reduction 问题简化

{已有一种方法求其他问题}

  • lcm(m, n) * gcd(m, n) = m * n {lcm: 最小公倍数, gcd: 最大公约数}
  • 求一个函数的最小值， 可以求一个函数负函数的最大值的负数

hash table 散列表

  • 需要把键在hash table 中尽可能均匀分布
  • 平均插入，删除， 查找效率都是 O(1), 当最坏情况全部冲突到一个位置时候，退化到 O(n)
  • open hasing, also: separate chaining 分离链 开hash
  • closed hashing 闭hash
  • double hashing
  • rehasing

B-tree B树

Dynamic Programming (DP) 动态规划

  • 与其对交叠的子问题一次又一次地求解，还不如对每个较小的子问题只求解一次并把结果记录在表中。 (对具有交叠子问题的问题进行求解的技术)
    • 类似斐波那契数

coins_row problem (求互不相临的最大金币总金额)

  • Time complexity: O(n), Space complexity: O(n)
1
2
3
4
5
def coin_row(coins):
    coin1, coin2 = coins[0], coins[1]
    for i, coin in enumerate(coins[2:]):
        coin1, coin2 = coin2, max(coin1 + coin, coin2)
    return coin2

change_making problem

  • Time complexity: O(mn), Space complexity: O(n)
1
2
3
4
5
6
7
8
9
10
11
def change_making(coins, change):
    count = [0] * change
    count[0] = 0
    for i in range(1, change):
        tmp = float('inf')
        j = 0
        while j <= len(coins) and j < len(coins) and i >= coins[j]:
            tmp = min(count[i - coins[j]], tmp)
            j += 1
        count[i] = tmp + 1
    return count[-1]

knapsack problem 背包问题

  • Time complexity: O(nW), Space complexity: O(nW)
  • #TODO

memory function 记忆功能

TODO

Greedy Technique 贪婪技术

Prim

  • 构造最小生成树算法
  • 先随机选一个点，每次扩展新的点使得这个新的点到已有点的距离最短，直到添加完所有顶点
1
# TODO (heaven)

Kruskal

  • 构造最小生成树算法
  • 先按照权重将边进行排序，然后不断把边加入子图，如果加入此边会产生回路，则天国，直到完成
1
# TODO (heaven)

Dijkstra

  • 单起点最短路径问题
1
# TODO (heaven)

Bit Operation

  • get bit
1
2
def is_git_i_1(num, i):
    return num & (1 << i) != 0
  • set bit
1
2
def set_bit(num, i):
    return num | (1 << i)
  • clear bit
1
2
3
def clear_bit(num, i):
    mask = ~(1 << i)
    return num & mask
  • update bit
1
2
3
def update_bit(num, i, v):
    mask = ~(1 << i)
    return (num & mask) | (v << i)

How To Optimaize the Algorithm

  • Optimaize & Solve Technique

    • Look for BUD
      • Bottlenecks
      • Unnecessary work
      • Duplicated work
    • DIY (Do It Yourself)
    • Simplify and Generalize
    • Base Case and Build (always use for recursion)
      • like for generate permutations 
        1
        2
        3
        1 Case "a" --> {"a"}
        2 Case "ab" --> {"ab", "ba"}
        3 Case "abc" --> {"cab", "acb", "abc", "cba", "bca", bac"}
    • Data structure brainstorm
      • hash
      • heap
      • tree

  • Consider the BCR (Best Conceivable Runtime)

    • The BCR is the best runtime you could conceive of a solution to a problem having.You can easily prove that there is no way you could beat the BCR.

  • Good coding looks like

    • correct
    • efficient
    • simple
    • readable
    • maintainable
      • use data structures generously
      • appropriate code resue
      • modular
      • flexible and robust
      • error checking

Power Table of 2

2^ = approximation approximate to
7 128
8 256
10 1024 one thousand 1K
16 65536 64K
20 1048576 one million 1MB
30 1073741824 one billion 1GB
32 4294967296 4GB
40 1099511627776 one trillion 1TB

Author: Min Gao

License: CC BY-NC-SA 4.0

如需转载或引用, 请标注出处。